In part one of this blog, the challenges facing ball bearings at high speed were outlined. SMT’s high-speed quasi-static model was described and some of its features explored in detail.
In this article, the focus turns to the dynamic modelling of ball bearings, and the benefits of this approach when analysing high-speed ball bearings.
Dynamic models provide the capability to undertake analyses of ball bearings in which temporal effects can be included and studied.
In ball bearings, these effects include the interaction between the elements and the cage, which in turn affects the behaviour of these component parts.
In MASTA 13, SMT released its own dynamic bearing model for ball bearing analysis, using a six-degree-of-freedom model for the elements, and a three-degree-of-freedom model for the cage.
The dynamic model uses the same underlying physical model for the elements as the quasi-static model discussed in part one, with the addition of impacts from the cage.
The cage is described by a model in which the cage can rotate and translate in the orbital plane of the elements, and can therefore come into contact with the elements and guiding ring.
In contrast with the quasi-static approach, which finds a combination of speeds and displacements which give force and moment equilibrium, the dynamic model calculates the forces and moments on the elements and cage for the speeds and displacements at the current timestep, and then applies the resultant accelerations.
A comprehensive set of time series results can be plotted, including all forces, moments, and components of power loss on each element and the cage.
The dynamic model allows us to compare and study several interesting effects, giving additional insight into the behaviour of a bearing under load compared to quasi-static analysis.
Comparing The Quasi Static and Dynamic Models Without A Cage
In this example, we applied a combined axial-radial load to an angular contact ball bearing, running at low speed (300 RPM) and high speed (10,000 RPM) and modelled the behaviour of this system using the quasi-static and dynamic models in MASTA.
The cage is not included in the dynamic analysis to allow the results of the two methods to be more directly compared.
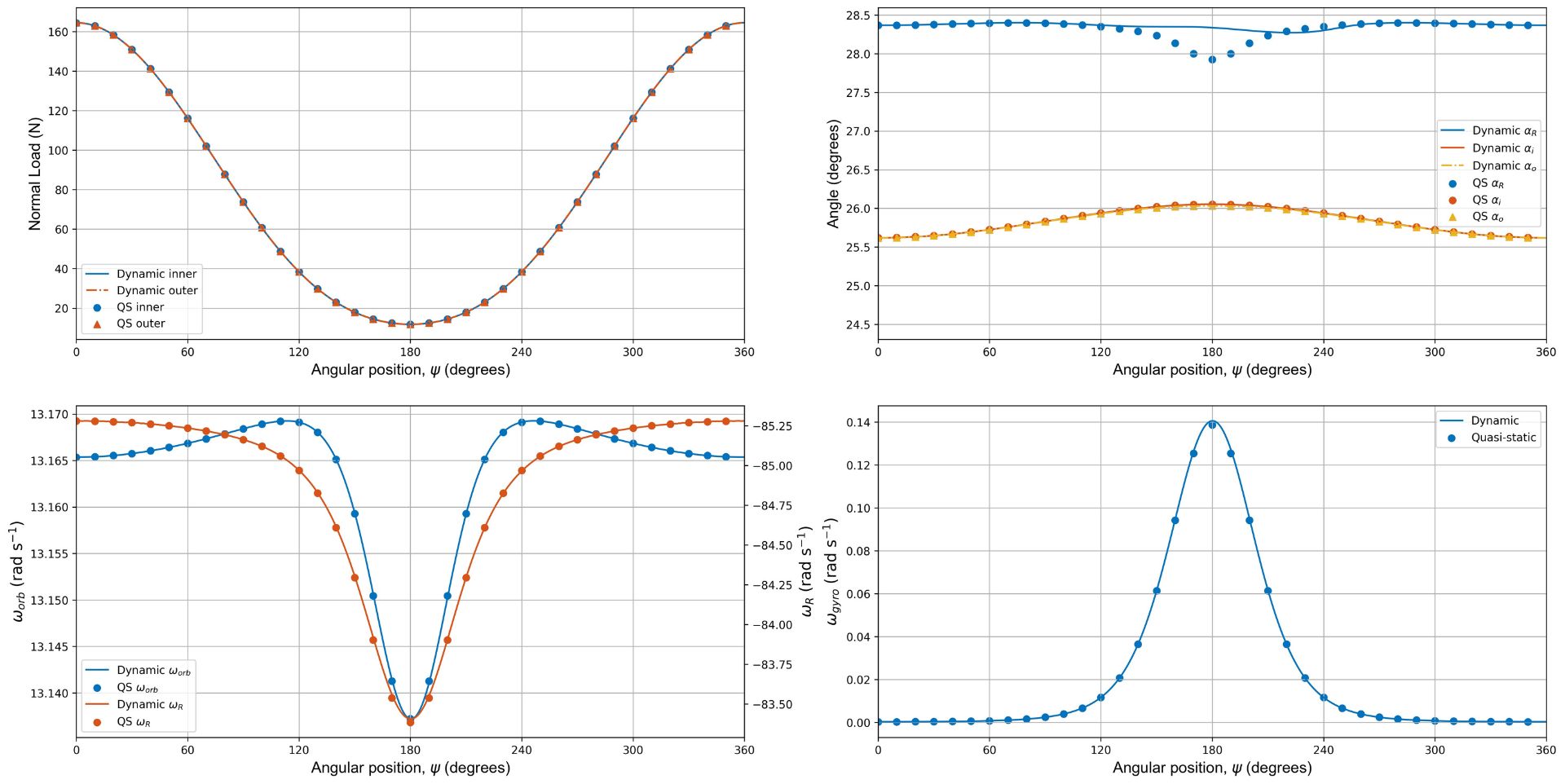
At low speed, there is good agreement between the quasi-static and dynamic models across all degrees of freedom of the elements.
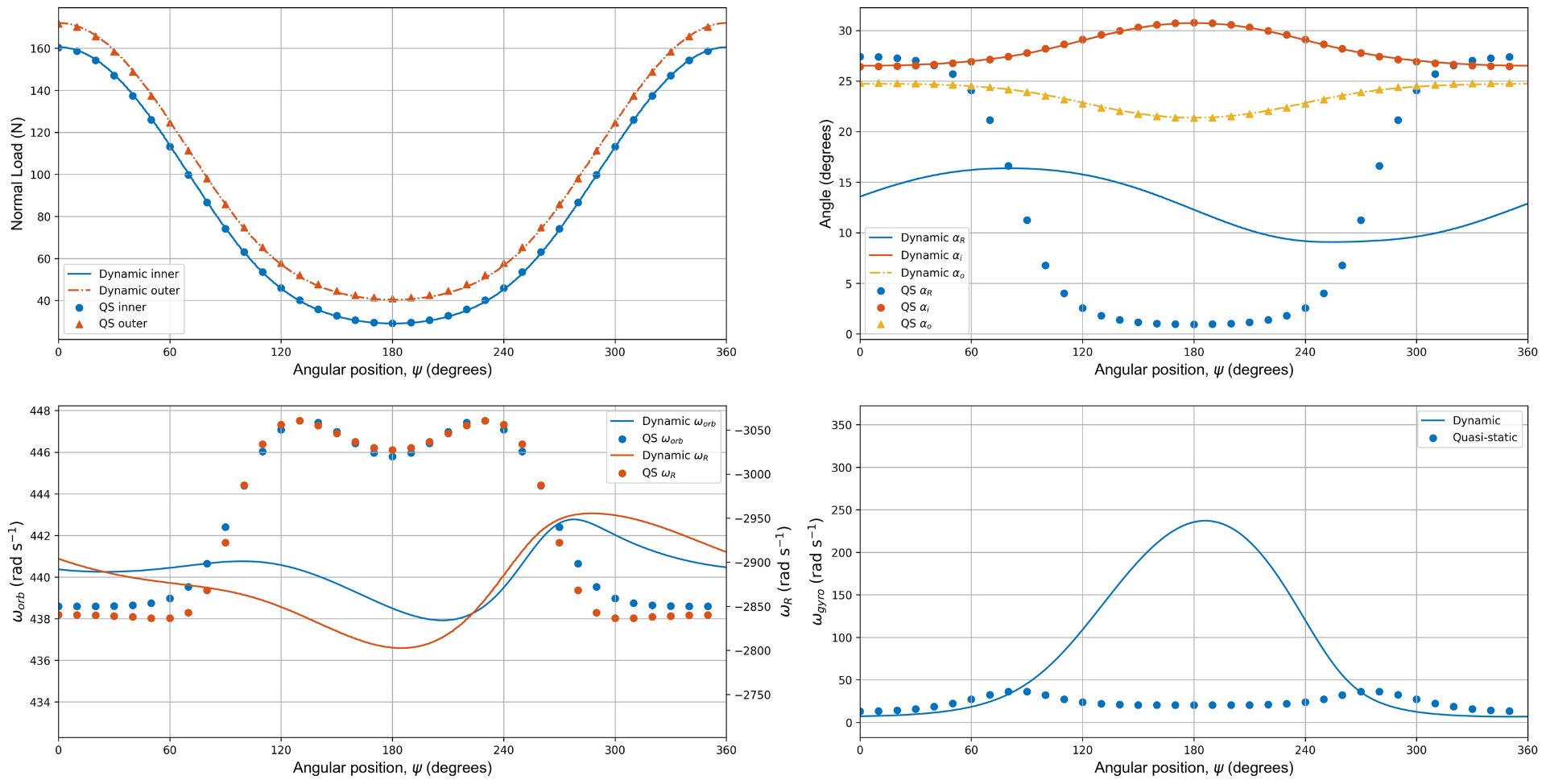
At high speed, whilst good agreement between the normal loads and contact angles can be seen (corresponding to the axial and radial displacements of the elements), discrepancies between the quasi-static and dynamic model for rotational properties of the element become apparent under these load conditions.
This is likely due to inertial effects on the elements; at high speed they are unable to respond to forces and moments quickly enough to always maintain a state close to equilibrium.
This demonstrates the additional accuracy provided by dynamic models for certain properties of the bearing, even when not considering the cage.
Comparison between the quasi-static and dynamic models for an angular contact ball bearing operating at low speed (ωi=300 RPM) under combined axial-radial load.
Comparison between the quasi-static and dynamic models for an angular contact ball bearing operating at high speed (ωi=10,000 RPM) under combined axial-radial load.
Effect and Analysis Of The Bearing Cage
Under a general radial load, the element orbit speed varies as the element moves around the raceway.
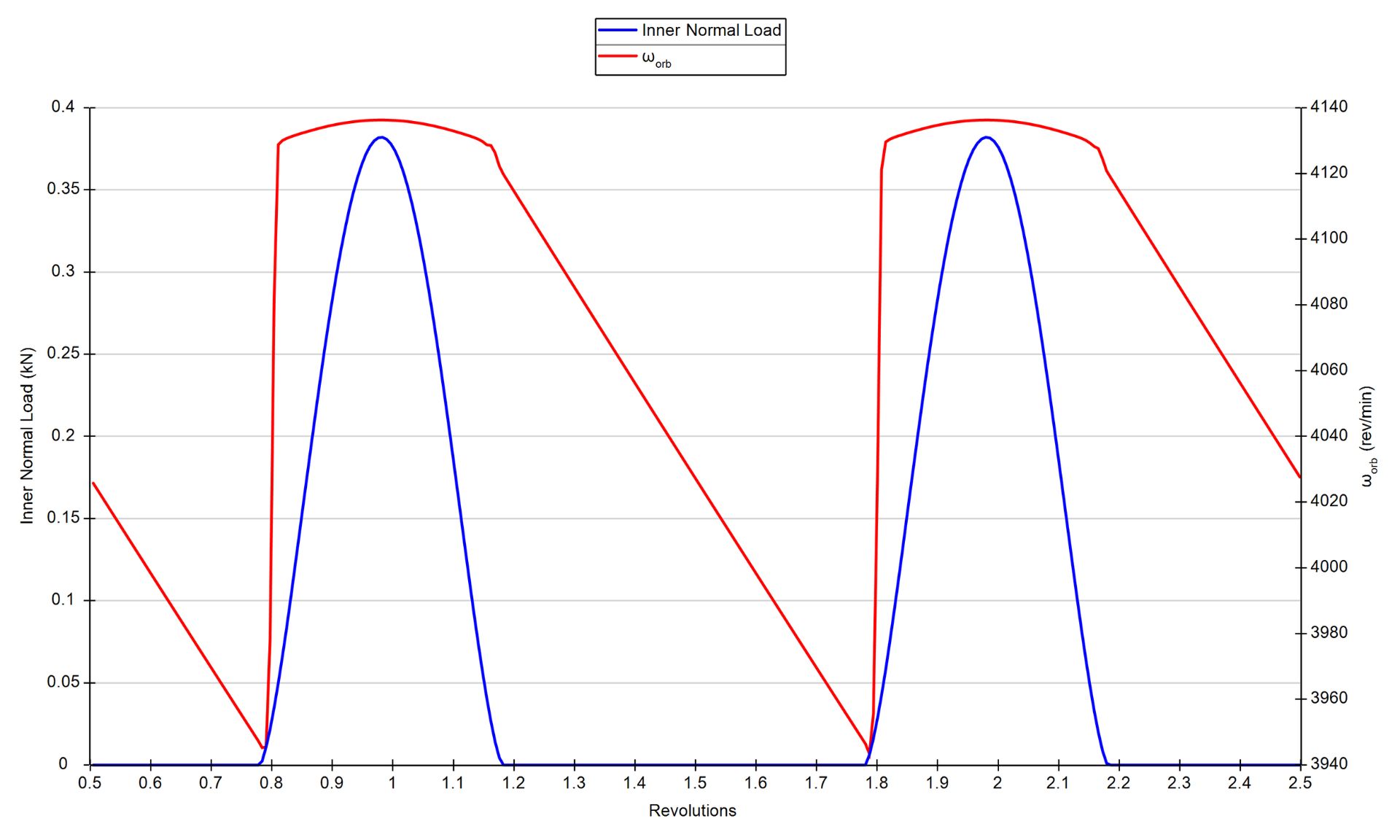
This can be seen most explicitly by dynamically modelling a radially loaded deep groove ball bearing without a cage.
Focussing on a single element, outside of the load zone, the element progressively slows due to hydrodynamic rolling forces acting against its motion.
Element orbit speed (in red) and normal load (in blue) for a radially loaded deep groove ball bearing with no cage.
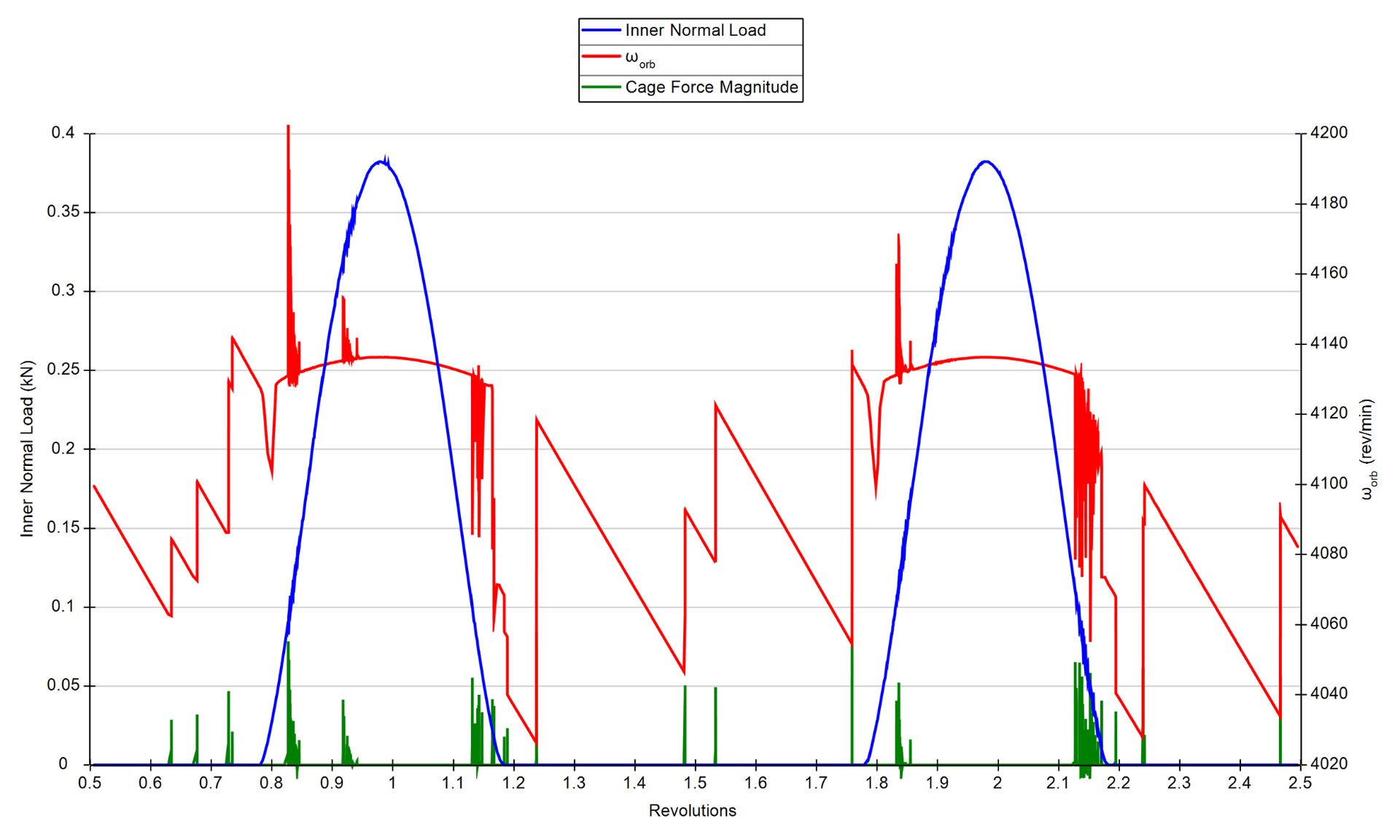
Inclusion of the cage model in the dynamic analysis significantly changes the results.
Outside of the load zone, the element again experiences the hydrodynamic rolling force, which acts to slow the element.
When the element speed slows such that the cage is travelling faster than the element, the clearance between the element and cage is taken up, and an impact occurs.
This impact increases the orbital velocity of the element and slows the orbital velocity of the cage; the cage is acting to push the elements in the unloaded zone.
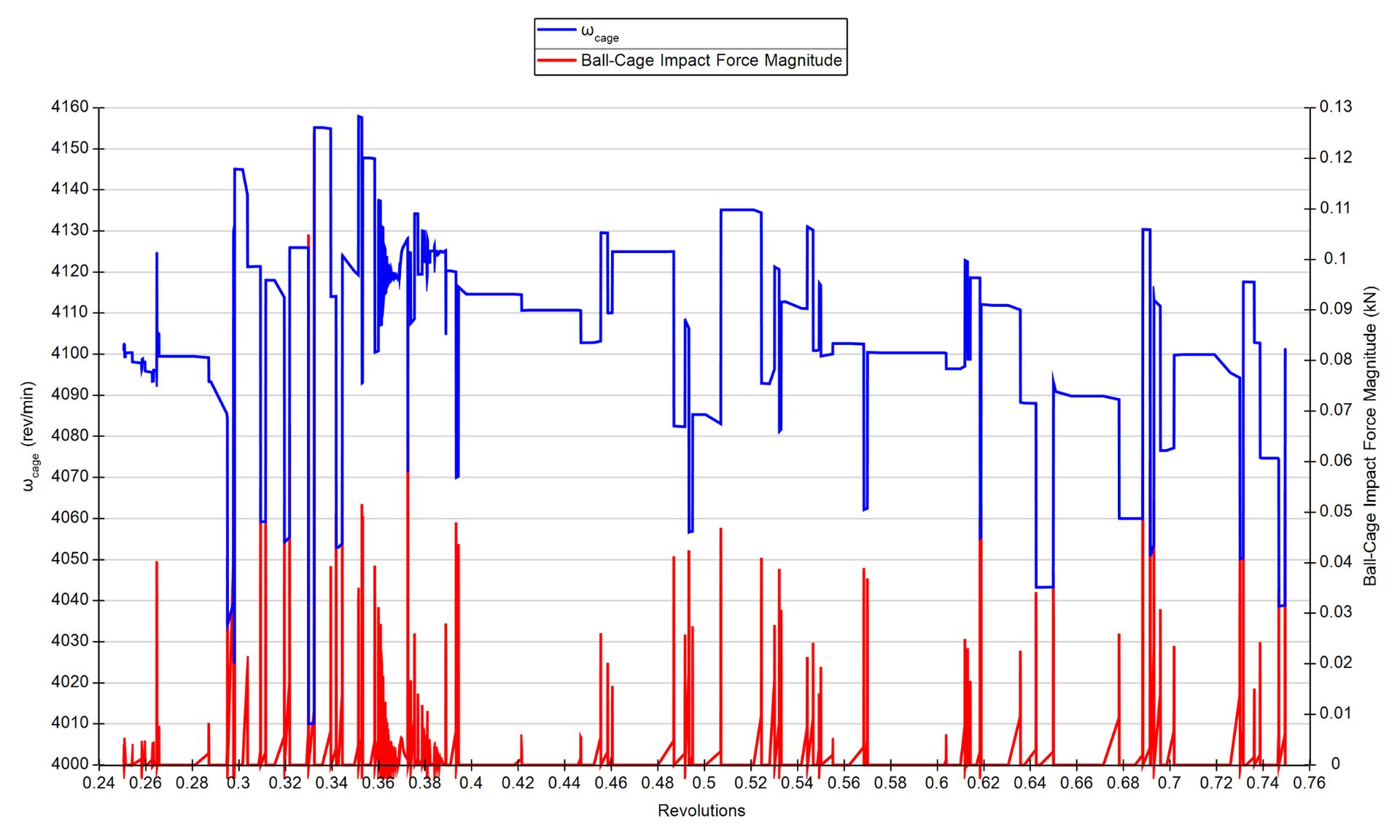
Element orbit speed (in red), normal load (in blue), and element-cage impact force (in green) for a radially loaded deep groove ball bearing. Impacts in the unloaded zone increase the element orbit speed.
The cage experiences impacts from multiple elements, and its orbit speed frequently changes; it reduces when an impact occurs with a more slowly moving element, and increases when an impact occurs with a more quickly moving element.
Ball-cage impacts (in red) and cage speeds (in blue) for a radially loaded deep groove ball bearing. The cage speed changes when there is an impact between the cage and an element.
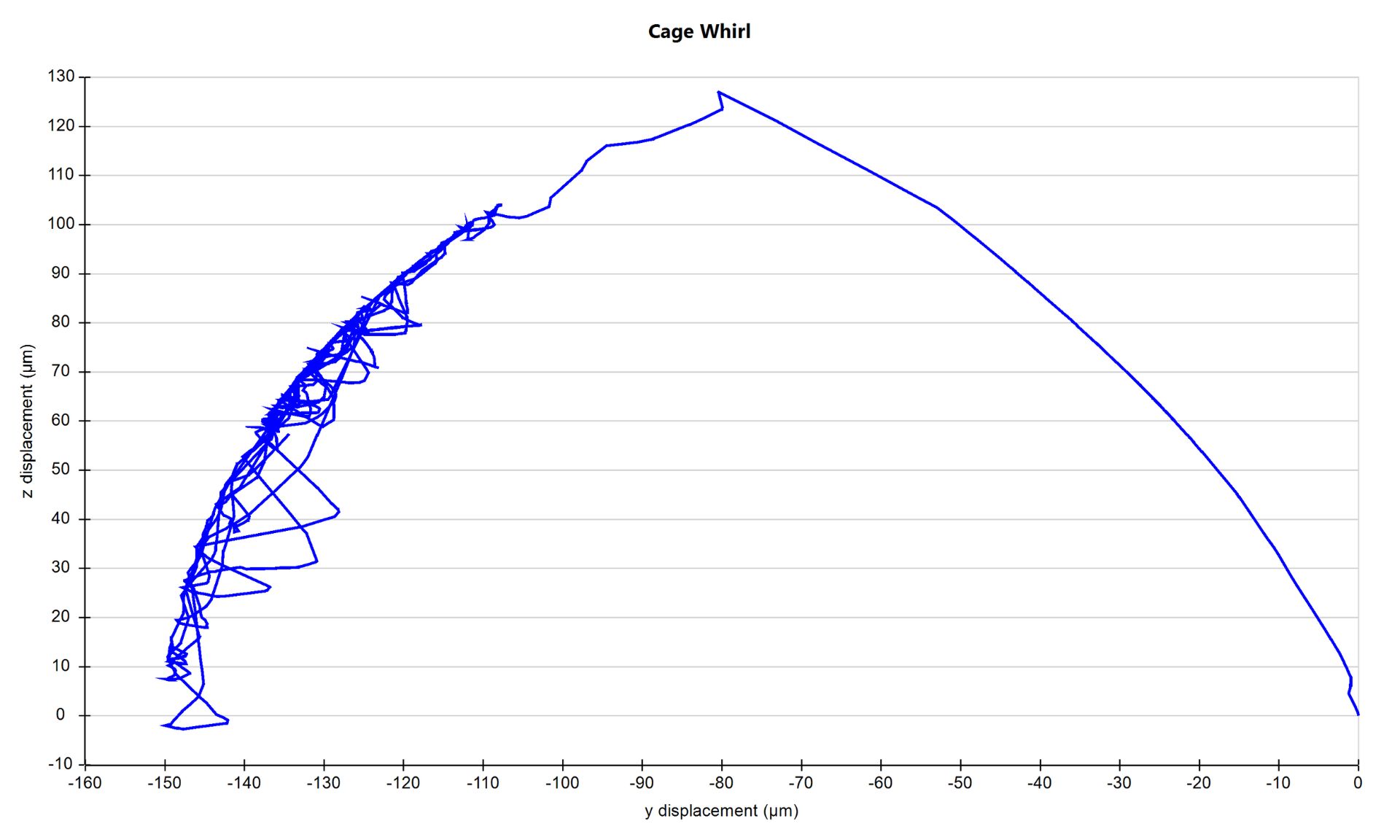
The impacts with the cage also cause the cage’s centre of mass position to change and we can plot this cage whirl within MASTA.
In this example, the pattern and direction of cage impacts causes the cage to displace away from a centred position, and subsequently oscillate in an arc.
Cage whirl in a radially loaded deep groove ball bearing.
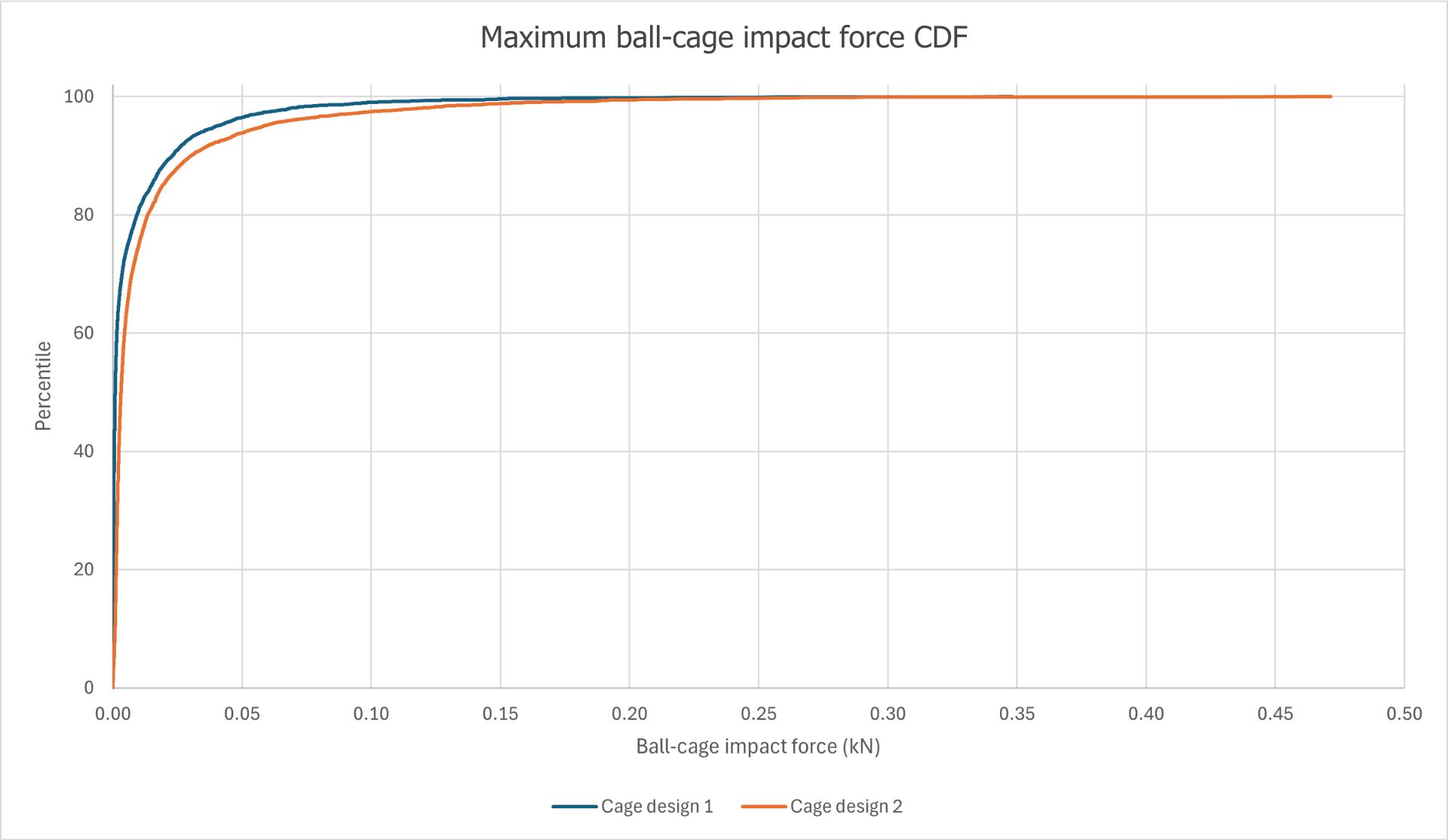
By taking the maximum force for each collision, MASTA can create a cumulative distribution function (CDF) for the ball-cage impacts, which can be used to compare cage impacts between different cage designs under the same loading conditions.
For example, in the figure below the CDF for ‘Cage design 2’ lies completely to the right of the CDF for ‘Cage design 1’; at every percentile, the ball-cage impact load on the second cage design is larger.
Cumulative distribution functions of two cage designs for a bearing under load.
Smearing
Smearing is a high-speed phenomenon caused by the contact between the element and the raceway and is most likely to occur as an element moves from an unloaded region to a loaded region.
MASTA includes a calculation for a smearing criterion at the contact,
smearing criterion = coefficient of friction × contact pressure × sliding velocity
which if it exceeds a value of 100 W/mm², indicates a risk of smearing.
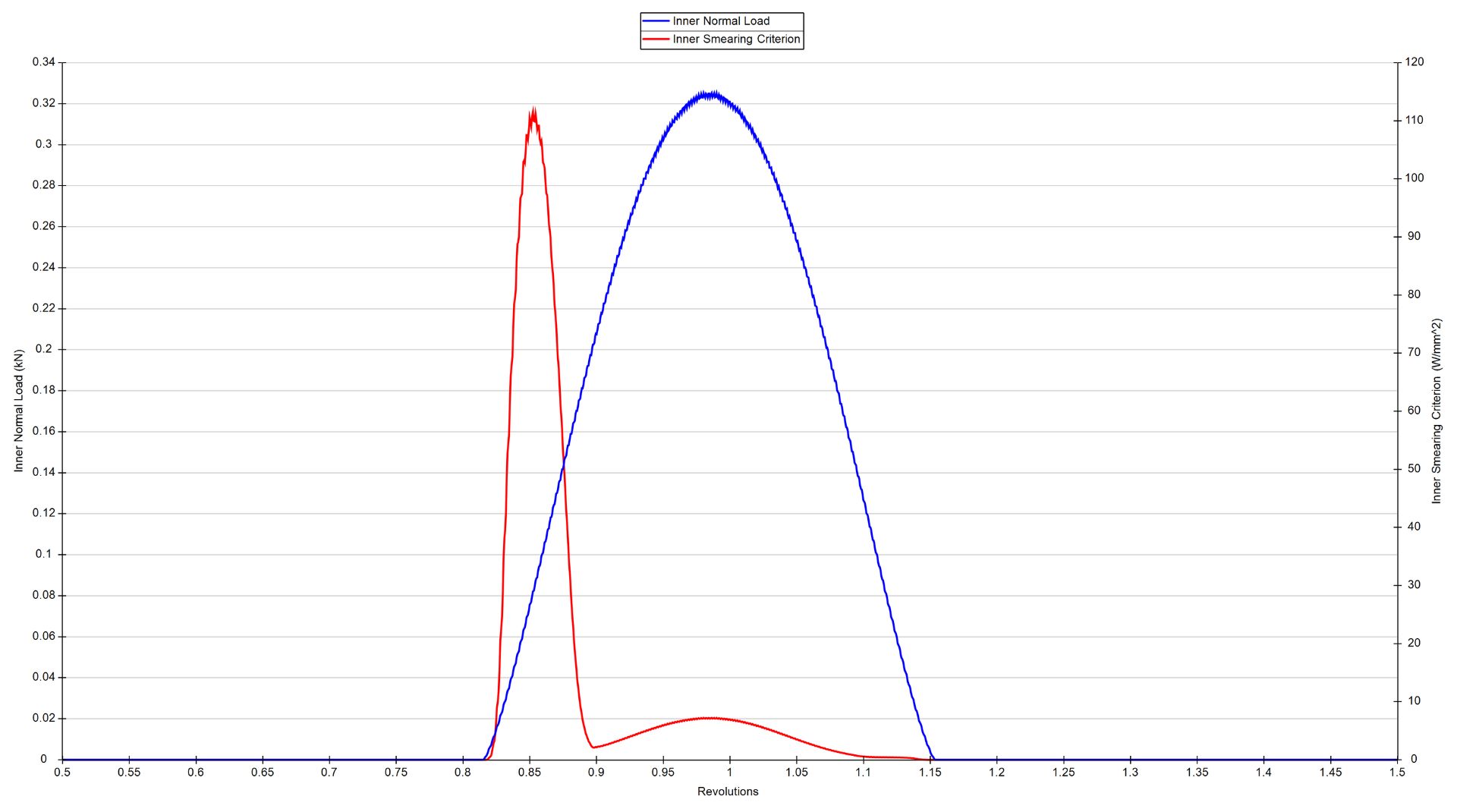
Smearing is best predicted using a dynamic model, as accurate calculation of the relative element-raceway sliding velocity through the transition from an unloaded to loaded zone cannot be made using quasi-static methods, as the element is temporarily far from equilibrium at this point.
Prediction of smearing in a radially loaded deep groove ball bearing. In this example, the smearing criterion (in red) increases rapidly on entry to the load zone (the normal load on the element is shown in blue).
Thank You For Reading
To summarise, we have described the dynamic bearing model implemented in MASTA 13 and demonstrated some of the advantages of undertaking dynamic analysis of ball bearings using this model.
Further details about the models underpinning the new high-speed ball bearing analysis can be found in two papers recently published by SMT in Tribology Transactions.
Tribological Models for Advanced Ball Bearing Simulation
Bearing Models for Advanced Ball Bearing Simulation
Related Blogs
High-Speed Ball Bearings – Challenges and Analysis
This article explores and focusses on the behaviour of ball bearings at high speed, but much of it is also relevant to roller bearings.