ブログのパート1では、ボールベアリングが高速で直面する課題について概略を説明しました。 また、SMT の高速準静的モデルについて説明し、その機能のいくつかを詳細に紹介しました。
このパートでは、ボールベアリングの動的モデルおよび高速ボールベアリングの解析におけるこのアプローチの利点に焦点を当てます。
動的モデルは、ボールベアリングの解析に時間的な影響を含めて検討する機能を提供します。
ボールベアリングでは、これらの影響にはボールと保持器間の相互作用が含まれ、それが構成部品の挙動に影響を与えます。
MASTA 13では、ボールに6自由度モデル、保持器に3自由度モデルを採用した、SMT独自のボールベアリング解析用動的モデルをリリースしました。
動的モデルでは、パート1で説明した準静的モデルと同様の物理モデルをボールに用い、保持器からの衝撃を加えています。
保持器は、ボールの軌道面内で回転および並進することができ、ボールやガイド輪と接触することができるモデルで定義されます。
力とモーメントの平衡を与える速度と変位の組み合わせを計算する準静的アプローチとは対照的に、動的モデルは、現在のタイムステップにおける速度と変位に対して、ボールと保持器にかかる力とモーメントを計算し、その結果得られる加速度を適用します。
個々のボールや保持器にかかるすべての力、モーメント、動力損失成分を含めた包括的な時系列結果を示すことが可能で す。
動的モデルを用いることで、いくつかの興味深い影響を比較・検討することができ、準静的解析と比較して、負荷時のベアリングの挙動についてさらなる洞察を得ることができます。
保持器なしの準静的モデルと動的モデルの比較
この事例では、低速(300 RPM)と高速(10,000 RPM)で回転するアンギュラボールベアリングにアキシアルとラジアル荷重の合成荷重を与え、MASTAの準静的モデルと動的モデルを用いてこのシステムの挙動をモデル化しました。
2つの手法の結果をより直接的に比較できるようにするため、保持器は動的解析に含めていません。
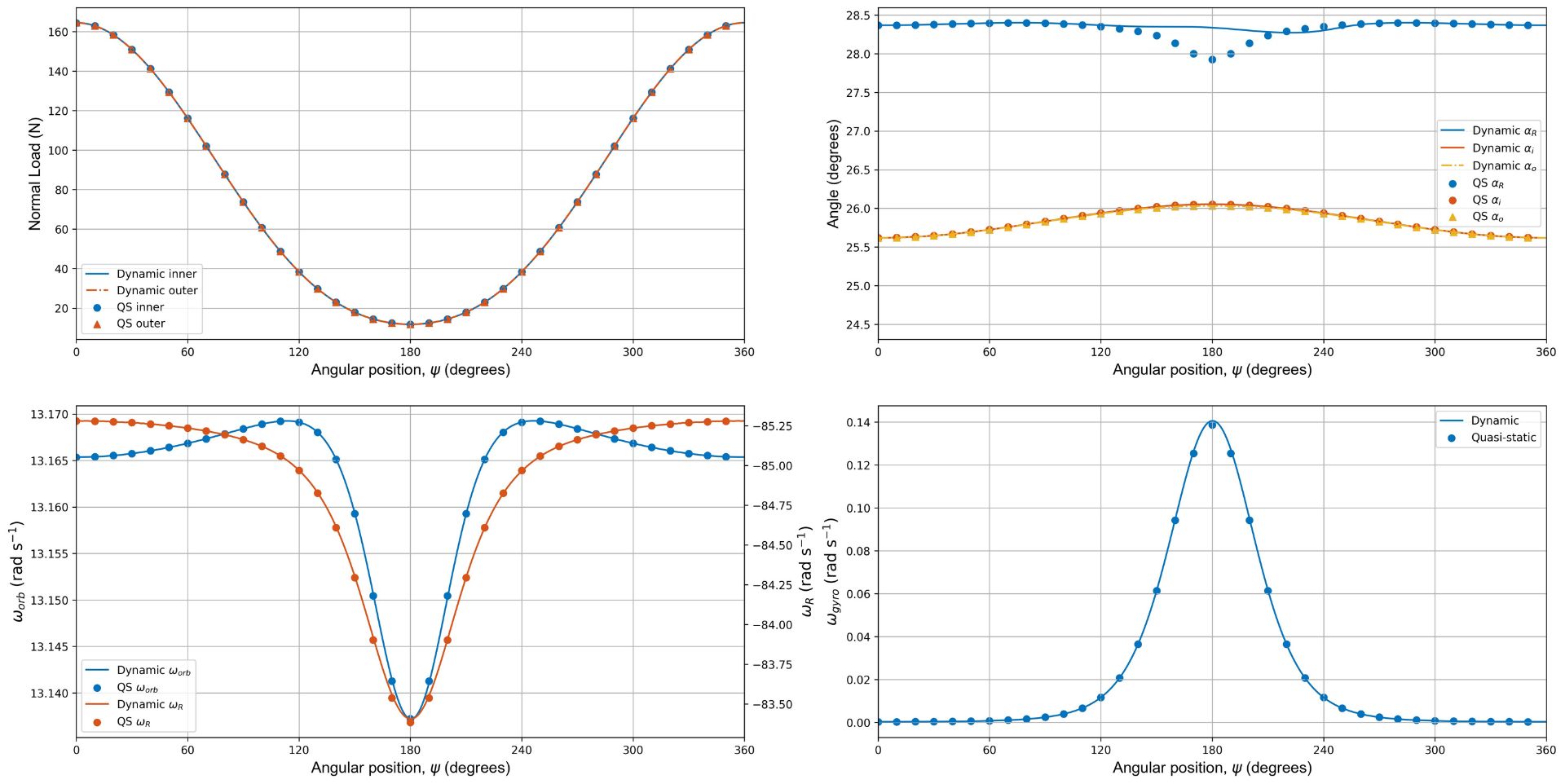
低速では、準静的モデルと動的モデルの間には、全てのボールの自由度でよく一致しました。
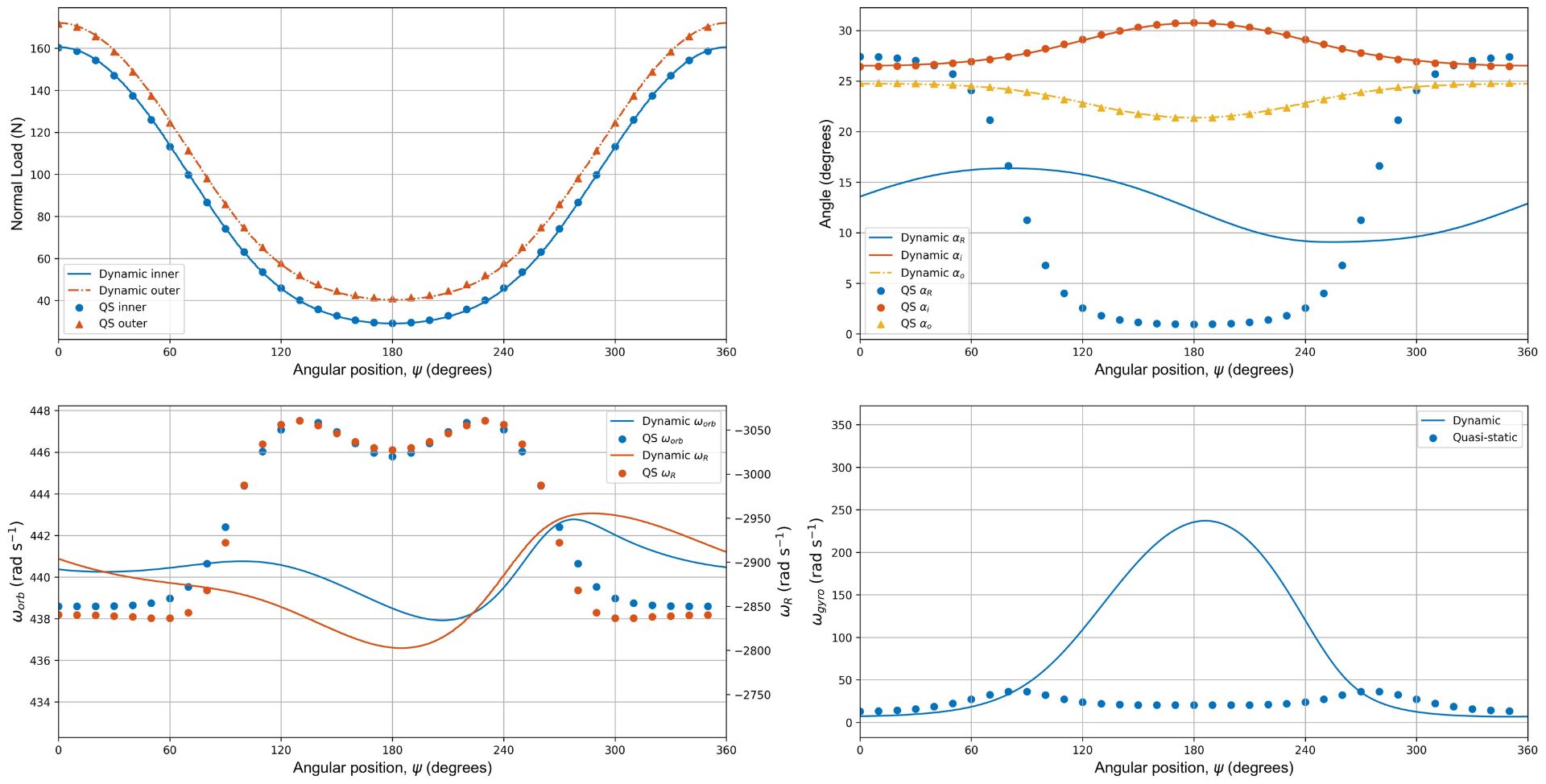
高速では、垂直荷重と接触角(ボールのアキシアル変位とラジアル変位に対応)の間で良好な一致が見られますが、これらの荷重条件下では、ボールの回転特性について準静的モデルと動的モデルの不一致が顕在化します。
これは、ボールにかかる慣性力の影響によるものと思われます。高速では、常に平衡に近い状態を維持できるほど素早く力やモーメントに反応することができないためです。
これは、保持器を考慮しない場合も、ベアリングのある特性に対して動的モデルが高い精度が得られることを示しています。
低速(ωi=300 RPM)で回転するアンギュラボールベアリングのアキシアル-ラジアル合成荷重下での準静的モデルと動的モデルの比較
高速(ωi=10,000 RPM)で回転するアンギュラボールベアリングのアキシアル-ラジアル合成荷重下での準静的モデルと動的モデルの比較
保持器の影響と解析
一般的なラジアル荷重の下では、ボールが軌道面を移動するにつれて、ボールの公転速度が変化します。
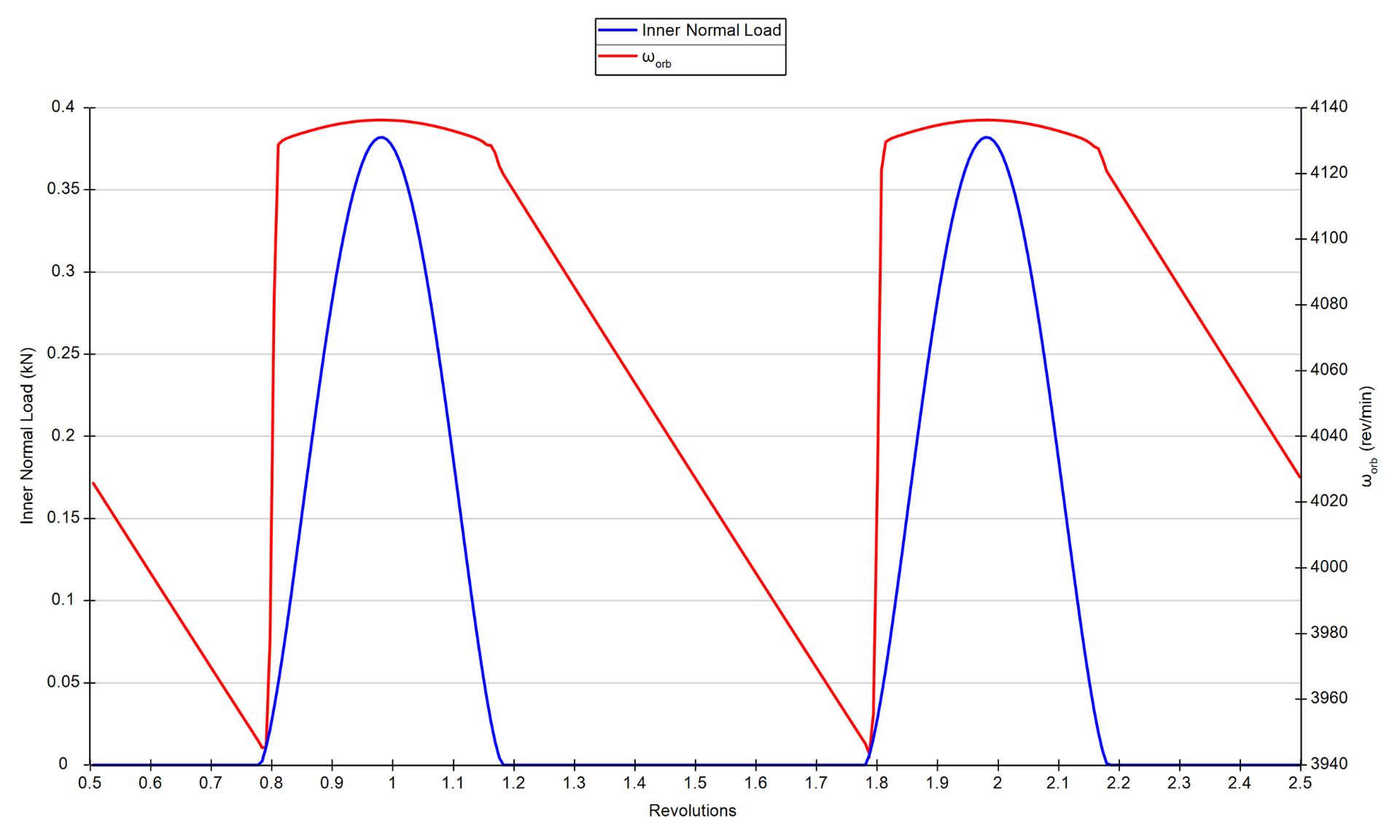
これは、保持器を含まないラジアル荷重を受ける深溝ボールベアリングを動的モデル化することで、はっきりとわかります。
負荷領域の外にある1つのボールに注目すると、ボールは、その運動に対して作用する流体転がり力によって徐々に減速していきます。
保持器なしのラジアル荷重を受ける深溝ボールベアリングのボール公転速度(赤)と垂直荷重(青)
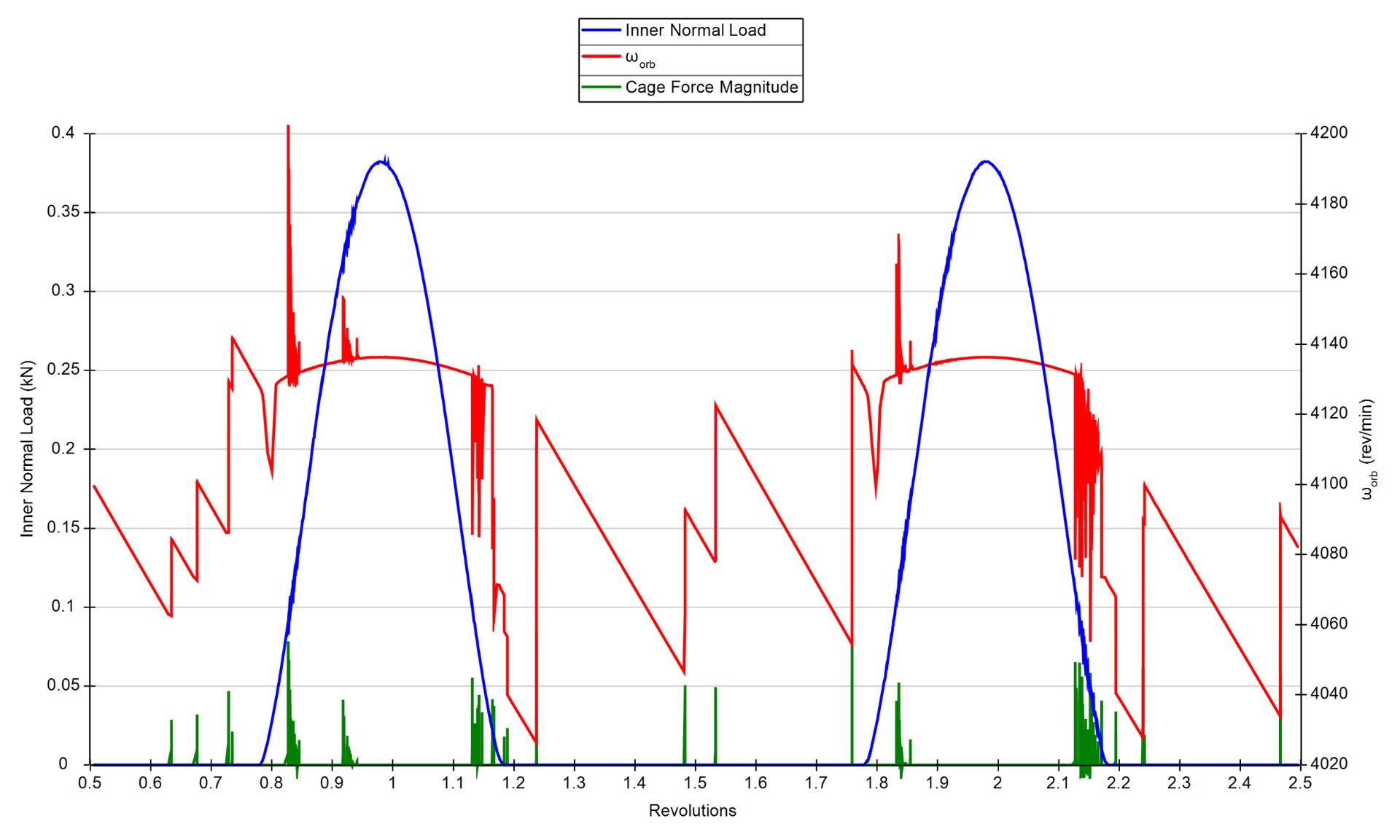
動的解析に保持器モデルを含めると、結果が大きく変わります。
負荷領域の外では、ボールは再び流体力学転がり力を受け、これはボールを減速させるように作用します。
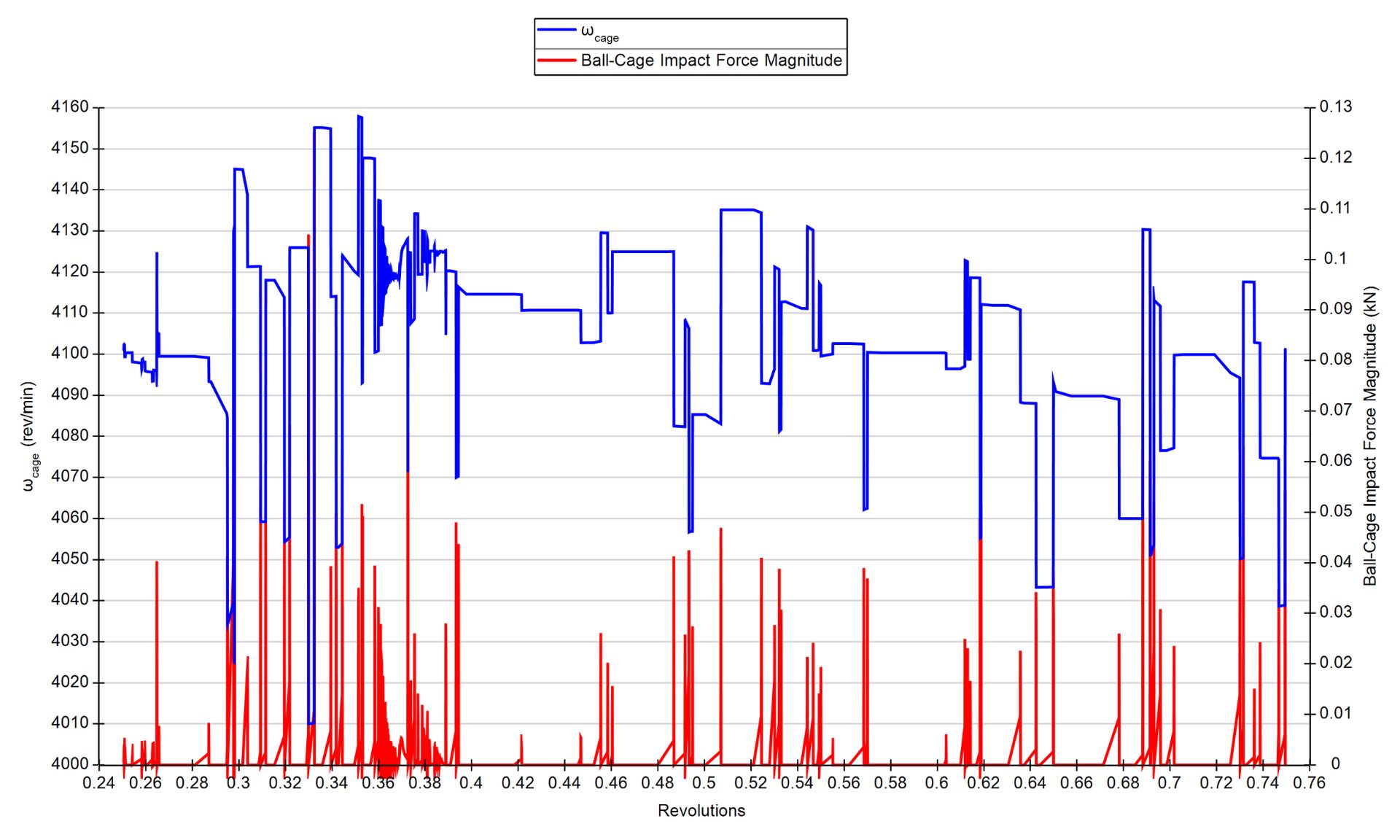
ボール公転速度が遅くなり、保持器がボールよりも速く回転するようになると、ボールと保持器の間のクリアランスがなくなり、衝突が発生します。
この衝突によってボールの公転速度が上がり、保持器の公転速度が遅くなります。保持器は無負荷領域でボールを押すように作用します。
ラジアル荷重を受ける深溝ボールベアリングのボール公転速度(赤)、垂直荷重(青)、ボール-保持器間の衝突力(緑)。無負荷領域での衝突はボール公転速度を増加。
保持器は複数のボールから衝突され、その公転速度は頻繁に変化します:遅い速度のボールと衝突した場合は減速し、速い速度のボールと衝突した場合は加速します。
ラジアル荷重を受ける深溝ボールベアリングのボール-保持器間の衝突(赤)と保持器速度(青)。保持器とボールの衝突により保持器速度が変化。
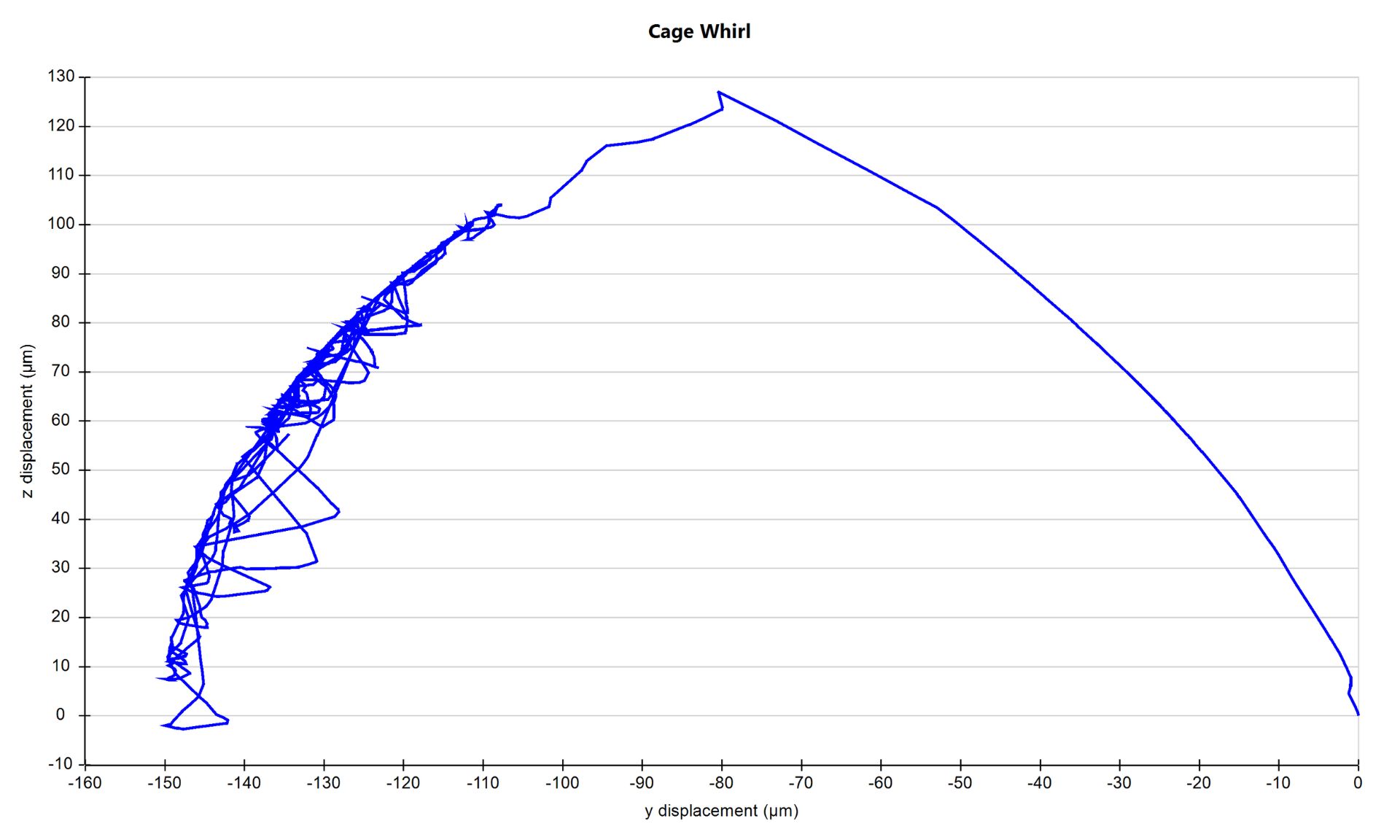
また、保持器への衝突によって保持器の重心位置が変化するため、MASTAではこの保持器の旋回状態をグラフ化することができます。
この事例では、保持器の衝突パターンと衝突方向によって、保持器は中心位置から移動し、その後弧を描いて振動します。
ラジアル荷重を受ける深溝ボールベアリングの保持器の旋回
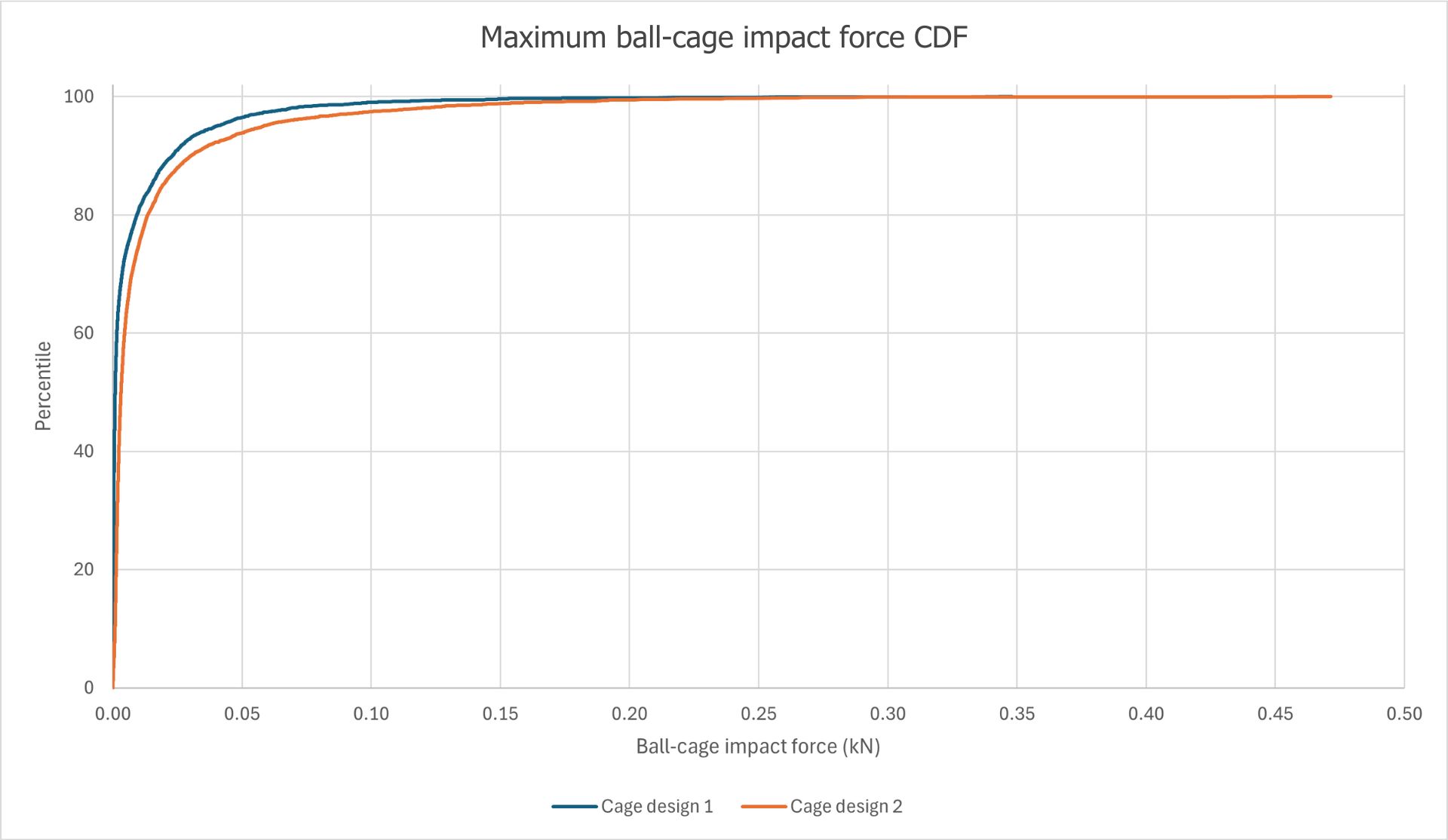
各衝突の最大力を求めることで、MASTAはボールと保持器の衝突の累積分布関数(CDF)を作成することができ、同じ負荷条件下で異なる保持器設計間の保持器衝突を比較することができます。
例えば、下図では「Cage design 2」の CDF は「Cage design 1」の CDF よりも完全に右側にあります。どのパーセンタイルでも、保持器設計 2 のボール-保持器の衝突荷重の方が大きくなります。
負荷を受けるベアリングに対する2つの保持器設計の累積分布関数
スミアリング
スミアリングは、ボールと軌道面の接触に起因して高速で発生する現象であり、ボールが無負荷領域から負荷領域に移動する際に最も発生しやすい。
MASTAには、接触部におけるスミアリング・クライテリアの計算も含まれています。
スメアリング・クライテリア = 摩擦係数 × 接触面圧 × すべり速度
この値が100W/mm²を超えると、スミアリングのリスクがあることを示します。
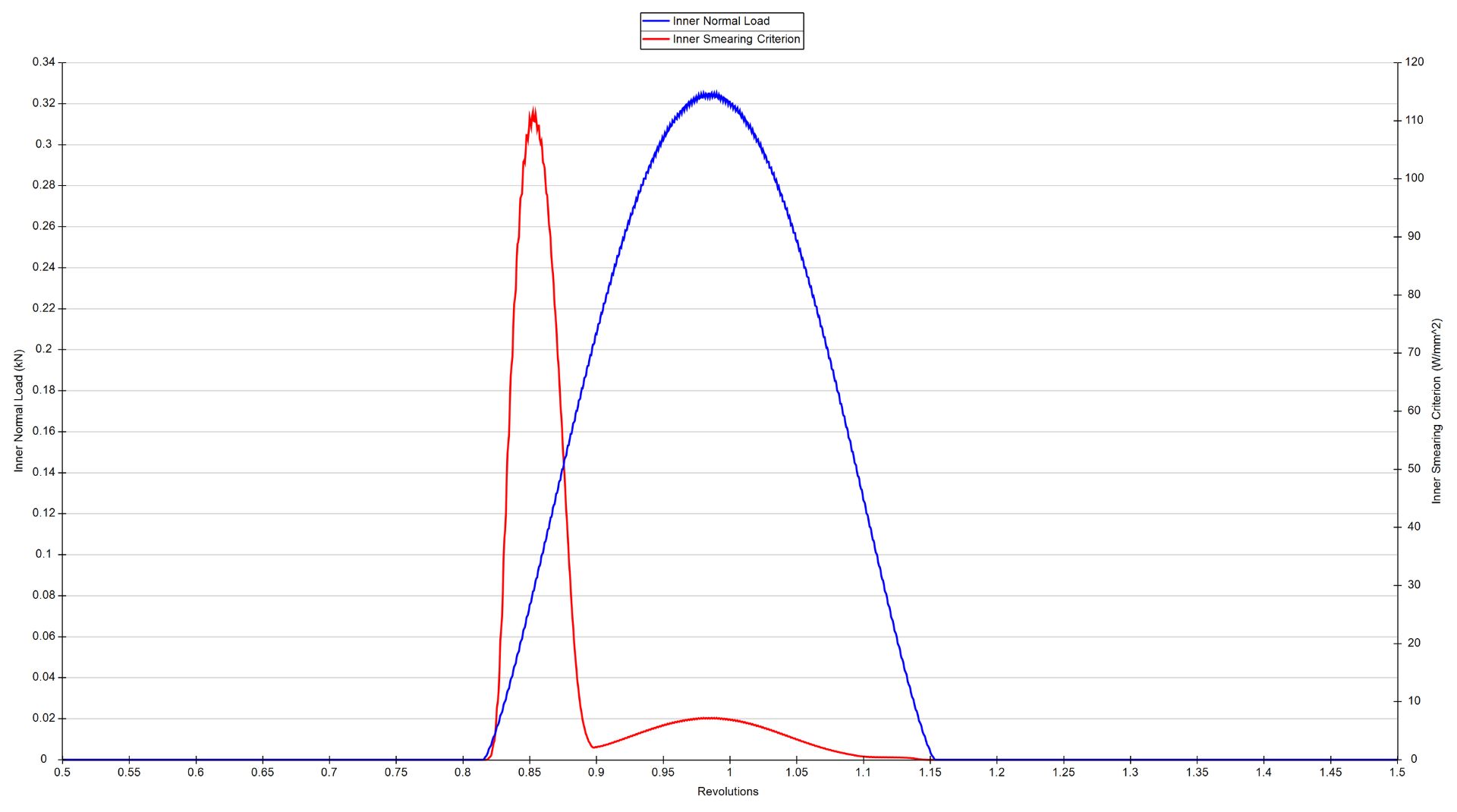
スミアリングは、動的モデルを用いて予測するのが最適です。なぜなら、無負荷領域から負荷領域への遷移に伴うボールと軌道の相対的なすべり速度の正確な計算は、準静的手法では計算できないためです。
ラジアル荷重を受ける深溝ボールベアリングのスミアリングの予測。この事例では、スミアリング・クライテリア(赤色)が負荷領域(ボールにかかる垂直荷重を青色で示す)に入ると急激に増加する。
お読みいただきありがとうございました
最後に、MASTA 13に採用されたベアリングの動的解析モデルについて説明し、このモデルを用いてベアリングの動的解析を行うことの利点をいくつか紹介しました。
新しい高速ボールベアリング解析を支えるモデルの詳細については、最近SMTがTribology Transactions誌に発表した2つの論文をご参照ください。
Tribological Models for Advanced Ball Bearing Simulation
Bearing Models for Advanced Ball Bearing Simulation
Related Blogs
高速ボールベアリング – 課題と解析
ここでは、高速回転におけるボールベアリングの挙動に焦点を当てますが、その多くはローラーベアリングにも当てはまります。